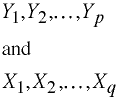
According to Webster
In the beginning...
Consider two sets of variables:
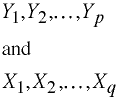
Construct
Construct the linear combinations:
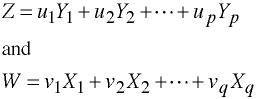
Such that rzw is a maximum.
Let
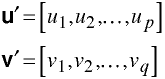
The XY Matrix
Consider a matrix XY made up of p Y's and q X's.

Partitioning the Covariance Matrix
Let S be the XY covariance matrix, thus,
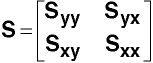
And
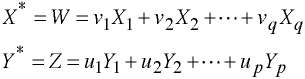
Thus, the sum of squared deviation scores can be obtained without transforming the raw scores.
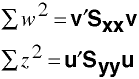
Criteria
Choose u and v such that
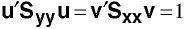
Compute
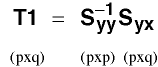
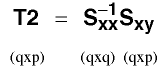
Now let
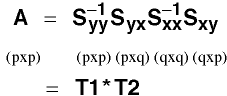
Let μi2 = eigenvalues of A
Let u = eigenvectors of A
Next let
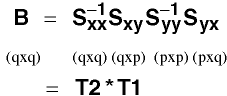
A & B will have the same eigenvalues.
Let v = eigenvectors of B.
Computing v
Let
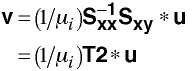
Canonical Correlation
Eigenvalues of A are canonical correlations squared, therefore
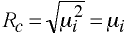
Computational Notes
Matrix A is not symmetric so we will need to go through some additional steps in order to get the eigenvalues and eigenvectors using the symeigen command.
1) C = Syx*Sxx-1*Sxy 2) F = cholesky(Syy-1) 3) D = F'*C*F 4) symeigen W L = D /* L has eigenvalues of A */ 5) U = F*W /* U has eigenvectors of A */
Remember the elements of L are μi2
Different Eigenvalues
Each canonical correlation has an eigenvalue related to Wilks' Lambda.
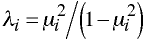
Tests of Significance
Wilks' Lambdas
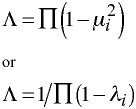
Compute m = n -3/2 - (p+q)/2 once.
The following are repeated with one being subtracted from p and q until either is equal to one. Thus,
First time p=3 q=5 Second time p=2 q=4 Third time p=1 q=3
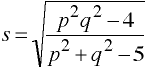
df1 = pq
df2 = ms - pq/2 + 1
Rao's F Approximation
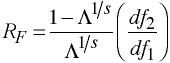
with df1 and df2 degrees of freedom.
Canonical Redundancy Coefficients
A measure of association between two sets of variables.
This measure is asymmetric:
R2x.y is the redundancy of set X given set Y
R2y.x is the redundancy of set Y given set X.
Canonical Redundancy Note
Rc2 is an estimate of the shared variance of two linear combinations of variables and not of the variance of the variables themselves. Thus, even when Rc2 is high, the redundancy of Y, X, or both may be very low.
Although it is always possible to compute both R2x.y and R2y.x, it is not always the case that both redundancy measures are meaningful. For example, when the Y variables are true dependent variables, R2y.x is useful while R2x.y does not make sense.
Redundancy
Each is a weighted sum of the squared canonical correlations, proportional to the aggregate variance of the variables in the set accounted for by successive canonical variates of that set.
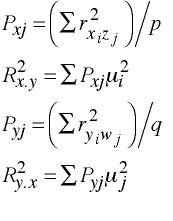
What Canonical Correlation Analysis Does...
Best
Questions concerning the number and nature of mutually independent relations (dimensions) between two sets of variables.
Mediocre
Questions concerning the degree of overlap or redundancy between two sets of variables.
Not Very Well
Questions concerning the similarity between two within-set correlation or covariance matrices.
Stata Example
Stata has completely rewritten their canonical correlation procedure in Stata 9.
use http://www.philender.com/courses/data/timm, clear
canon (apt ppvt rpmt) (n s ns na ss), test(1 2 3)
Linear combinations for canonical correlations Number of obs = 37
------------------------------------------------------------------------------
| Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
u1 |
apt | .0032264 .0082904 0.39 0.699 -.0135873 .02004
ppvt | .0762248 .0152914 4.98 0.000 .0452124 .1072372
rpmt | .0141323 .0588196 0.24 0.811 -.1051594 .1334239
-------------+----------------------------------------------------------------
v1 |
n | -.0071509 .082705 -0.09 0.932 -.1748843 .1605826
s | -.0756585 .0465969 -1.62 0.113 -.1701612 .0188443
ns | -.0353218 .0450604 -0.78 0.438 -.1267084 .0560649
na | .1579155 .051318 3.08 0.004 .0538377 .2619933
ss | .0435563 .0544885 0.80 0.429 -.0669515 .154064
-------------+----------------------------------------------------------------
u2 |
apt | -.033176 .0151245 -2.19 0.035 -.06385 -.002502
ppvt | -.0016715 .0278969 -0.06 0.953 -.058249 .054906
rpmt | .2756473 .1073075 2.57 0.014 .0580176 .493277
-------------+----------------------------------------------------------------
v2 |
n | .1599911 .1508828 1.06 0.296 -.1460134 .4659955
s | .042124 .0850089 0.50 0.623 -.1302821 .2145302
ns | .2381605 .0822059 2.90 0.006 .0714393 .4048817
na | -.0594188 .093622 -0.63 0.530 -.2492931 .1304555
ss | -.1823911 .099406 -1.83 0.075 -.3839959 .0192137
-------------+----------------------------------------------------------------
u3 |
apt | .0358057 .030764 1.16 0.252 -.0265865 .0981979
ppvt | -.0482553 .0567435 -0.85 0.401 -.1633363 .0668258
rpmt | .2104353 .2182681 0.96 0.341 -.232233 .6531035
-------------+----------------------------------------------------------------
v3 |
n | .0992871 .3069021 0.32 0.748 -.5231393 .7217135
s | .1746239 .1729119 1.01 0.319 -.1760577 .5253054
ns | -.0100806 .1672103 -0.06 0.952 -.3491988 .3290376
na | -.2290303 .1904313 -1.20 0.237 -.6152428 .1571822
ss | .2019493 .2021962 1.00 0.325 -.2081236 .6120222
------------------------------------------------------------------------------
(Standard errors estimated conditionally)
Canonical correlations:
0.7165 0.4906 0.2668
----------------------------------------------------------------------------
Tests of significance of all canonical correlations
Statistic df1 df2 F Prob>F
Wilks' lambda .343169 15 80.4576 2.5381 0.0039 a
Pillai's trace .825289 15 93 2.3529 0.0066 a
Lawley-Hotelling trace 1.44876 15 83 2.6722 0.0023 a
Roy's largest root 1.05512 5 31 6.5417 0.0003 u
----------------------------------------------------------------------------
Test of significance of canonical correlations 1-3
Statistic df1 df2 F Prob>F
Wilks' lambda .343169 15 80.4576 2.5381 0.0039 a
----------------------------------------------------------------------------
Test of significance of canonical correlations 2-3
Statistic df1 df2 F Prob>F
Wilks' lambda .705252 8 60 1.4308 0.2025 e
----------------------------------------------------------------------------
Test of significance of canonical correlation 3
Statistic df1 df2 F Prob>F
Wilks' lambda .92883 3 31 0.7918 0.5078 e
----------------------------------------------------------------------------
e = exact, a = approximate, u = upper bound on F
canon, stdcoef
Canonical correlation analysis Number of obs = 37
Standardized coefficients for the first variable set
| 1 2 3
-------------+------------------------------
apt | 0.0713 -0.7332 0.7913
ppvt | 0.9548 -0.0209 -0.6044
rpmt | 0.0437 0.8531 0.6513
--------------------------------------------
Standardized coefficients for the second variable set
| 1 2 3
-------------+------------------------------
n | -0.0211 0.4719 0.2928
s | -0.3835 0.2135 0.8850
ns | -0.2244 1.5132 -0.0640
na | 1.1438 -0.4304 -1.6589
ss | 0.2774 -1.1618 1.2864
--------------------------------------------
Canonical correlations:
0.7165 0.4906 0.2668
estat correlations
Correlations for variable list 1
| apt ppvt rpmt
-------------+------------------------------
apt | 1.0000
ppvt | 0.3703 1.0000
rpmt | 0.2114 0.3548 1.0000
--------------------------------------------
Correlations for variable list 2
| n s ns na ss
-------------+--------------------------------------------------
n | 1.0000
s | 0.4007 1.0000
ns | 0.5370 0.3523 1.0000
na | 0.6481 0.6478 0.7136 1.0000
ss | 0.6704 0.4252 0.7695 0.7951 1.0000
----------------------------------------------------------------
Correlations between variable lists 1 and 2
| apt ppvt rpmt
-------------+------------------------------
n | 0.1860 0.4444 0.3504
s | 0.1609 0.2682 0.2386
ns | 0.0685 0.4692 0.4388
na | 0.2617 0.6720 0.3390
ss | 0.3341 0.5876 0.3404
--------------------------------------------
estat loadings
Canonical loadings for variable list 1
| 1 2 3
-------------+------------------------------
apt | 0.4341 -0.5606 0.7052
ppvt | 0.9967 0.0102 -0.0803
rpmt | 0.3976 0.6906 0.6041
--------------------------------------------
Canonical loadings for variable list 2
| 1 2 3
-------------+------------------------------
n | 0.6320 0.3122 0.4004
s | 0.3879 0.1630 0.4521
ns | 0.6588 0.6406 0.2112
na | 0.9422 0.1697 0.0814
ss | 0.8371 0.0675 0.4906
--------------------------------------------
Correlation between variable list 1 and canonical variates from list 2
| 1 2 3
-------------+------------------------------
apt | 0.3111 -0.2750 0.1881
ppvt | 0.7142 0.0050 -0.0214
rpmt | 0.2849 0.3388 0.1612
--------------------------------------------
Correlation between variable list 2 and canonical variates from list 1
| 1 2 3
-------------+------------------------------
n | 0.4529 0.1532 0.1068
s | 0.2780 0.0800 0.1206
ns | 0.4721 0.3143 0.0563
na | 0.6751 0.0833 0.0217
ss | 0.5998 0.0331 0.1309
--------------------------------------------
canred 1 /* findit canred */
Canonical redundancy analysis for canonical correlation 1
Canonical correlation coefficient 0.7165
Squared canonical correlation coefficient 0.5134
own opposite
Proportion of standardized variance variate variate
of u variables with ... 0.4467 0.2293
of v variables with ... 0.5145 0.2641
canred 2 /* findit canred */
Canonical redundancy analysis for canonical correlation 2
Canonical correlation coefficient 0.4906
Squared canonical correlation coefficient 0.2407
own opposite
Proportion of standardized variance variate variate
of u variables with ... 0.2638 0.0635
of v variables with ... 0.1136 0.0273
Multivariate Course Page
Phil Ender, 2may05, 29Jan98