The Matrix

• An element of A is a_ij
• a_ij is called the ijth element of A

Multiplication by a Scalar

• Multiply each element of the matrix by the scalar.

• Let c = 3

  

Matrix Addition & Subtraction

• Add each element of the first matrix to the corresponding element of the second matrix.

• In order to add matrices, the matrices must have the same dimensions.

  

• Note: A+B = B+A -- commutative law

• Note: A+(B+C) = (A+B)+C -- associative law

Matrix Multiplication

Notes

• Note: In general, A*B does not equal B*A -- matrix multiplication is not commutative

• Note: (A*B)*C = A*(B*C) -- associative law

• Note: A*(B+C) = A*B + A*C
• And: (B+C)*A = B*A + C*A -- distributive law

Transpose of a Matrix

• Mathematical notation -> X'

  

  Notes

  • (A')' = A

  • (A*B)' = B' * A'
    Note the reverse order of the matrix multiplication

  Common Vectors

  Column Vectors

  

  Row Vector

  

  Unit Vector

  • Denoted as u or 1

    

  Common Matrices

  Vertical Matrix

  

  Horizontal Matrix

  

  Unit Matrix

  • Denoted as U or 1

    

  Square Matrix

  • Note: The number of rows equals the number of columns

    

  Diagonal Matrix

  

  Identity Matrix

  • Denoted as I

    

  • Remember I*A = A*I = A

  Symmetric Matrix

  
  • Remember C = C'

Triangular Matrix

Inverse of a Matrix

• Mathematical notation: B = A^-1

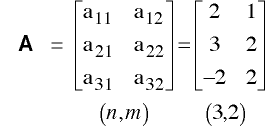
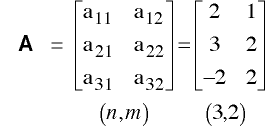
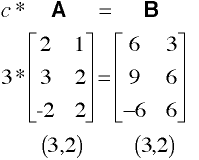
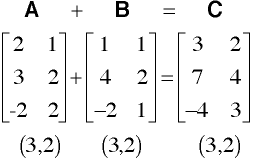
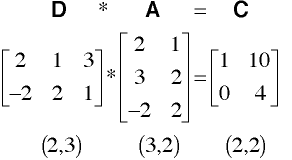
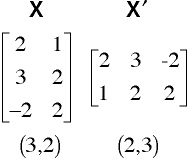
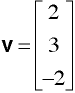
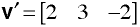
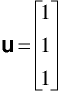
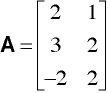
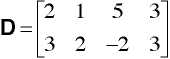
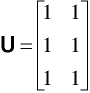
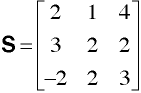
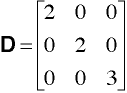
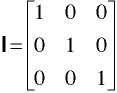
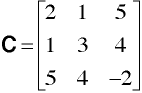
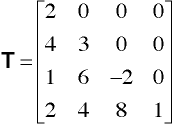
  -must be a square matrix

• Remember A^-1 * A = A * A^-1 = I

• In scalar terms: a^-1 = 1/a

  And 1/a * a = a * 1/a = 1

Inversion by Hand

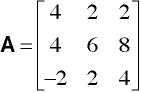
First we will augment Matrix A with an identity matrix and call the result A₀.

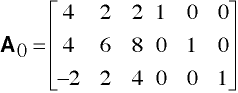
We will also need an identity matrix called I₀.

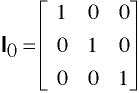
Step 1

Now we will work on the first column of I₀. The diagonal element in the first column of A₀ is called the pivot. We will replace the first diagonal element of I₀ with 1/a₁₁. Then we will replace the non-pivot elements with -a_ij/a₁₁ and call the result I₁.
Compute A₁ = I₁ * A₀.

Step 2

Now we repeat the process by modifying the second column of I₀. This time the pivot value is the 22 element. The new matrix is called I₂.
Compute A₂ = I₂ * A₁.

Step 3

Lastly we repeat the process by modifying the third column of I₀. This time the pivot value is the 33 element. The new matrix is called I₃.
Compute A₃ = I₃ * A₂.

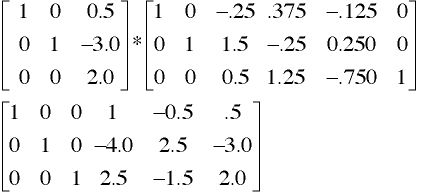
The last three columns of A₃ are the inverse of A, thus:

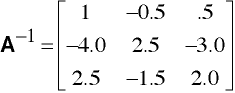
Mata Example:

i=I(3)
a = (4,2,2\4,6,8\-2,2,4)
a

a = a,i
a

i1 = (.25,0,0\-1,1,0\.5,0,1)
i1

i2 = (1,-.125,0\0,.25,0\0,-.75,1)
i2
         
i3=(1,0,.5\0,1,-3\0,0,2)
i3

ainv = i3*i2*i1*a
ainv

ainv = ainv[1..., 4..6]
ainv

Determinant of a Matrix

• The fundamental geometric meaning of the determinant is as the scale factor for volume when matrix A is regarded as a linear transformation.

• Mathematical notation: d = |A|

Example: Inverse & Determinant of a Matrix

Computing Column & Row Sums

• Column Sums:
  • Using matrix arithmetic: T = U'*X

        U'   *   X   =   T
     [1 1 1] * |3 1|
               |2 0| = [7 5]
               |2 4|
               
      (1,3)    (3,2)   (1,2)

• Row Sums:
  • Using Matrix arithmetic: T = X*U

       X   *  U   =  T
     |3 1|   |1|    |4|
     |2 0| * |1| =  |2|
     |2 4|          |6|
     
     (3,2)  (2,1)  (3,1)

Horizontal Concatenation

Vertical Concatenation (Appending)

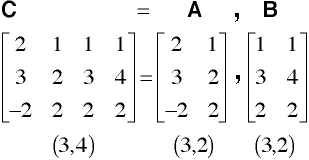
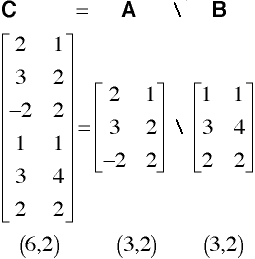
Multivariate Course Page