ED230B/C: Multilevel Data Issues

Multilevel Data Issues -- Page 2

Eta Squared

Eta squared is equal to R² when doing regression using coded vectors for group membership.

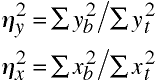
Correlations Again

Using eta squared the formulas for the correlations can be rewritten as:

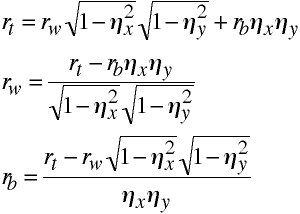
Regression Coefficients Again

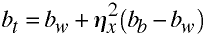
An Example

Source Σy² Σx² Σxy r b
Total 82.5 42.5 37.5 .633 .88235
G1 10.0 10.0 0 0 0
G2 10.0 10.0 0 0 0
Within 20.0 20.0 0 0 0
Between 62.5 22.5 37.5 1.00 1.667

Source	Σy²	Σx²	Σxy	r	b
Total	82.5	42.5	37.5	.633	.88235
G1	10.0	10.0	0	0	0
G2	10.0	10.0	0	0	0
Within	20.0	20.0	0	0	0
Between	62.5	22.5	37.5	1.00	1.667

eta²_y = .75758
eta²_x = .52941

Multilevel Analysis

Some argue that the issue is not appropriate unit of analysis but development of appropriate techniques that will make full use of information from different levels.

The choice of one level to the exclusion of others may result in masking certain effects or in indicating effects when none exist.

Multilevel analyses are most important when individuals are nested within groups and groups are nested within larger units.

Say, students nested in classes and classes nested in schools.

Some processes work on individuals while others work on groups.

(Cronbach & Webb, 1975) - High mean aptitude of a class may lead a teacher to crowd more material into the course, thereby leading to either greater or lesser achievement for the class as a whole.

"...the experience of a student with an IQ of 110 depends on whether the class mean is 100 or 120."

Multilevel data analysis is currently one of the hottest research areas.

The program HLM (Hierarchical Linear Models) is the most commonly used multilevel data analysis in the US. HLM was developed by Bryk and Radenbush.

Really cutting edge work is being done with multilevel analysis of latent variables (structural equation models).

Stata Example

The sch10 dataset contains data on students in 10 schools.

use http://www.gseis.ucla.edu/courses/data/sch10
rename scid school

table school, cont(freq mean math mean hmwk) format(%6.2f)

----------------------------------------------
group(sch |
id)       |      Freq.  mean(math)  mean(hmwk)
----------+-----------------------------------
        1 |         23       45.74        1.39
        2 |         20       42.15        2.35
        3 |         24       53.25        1.83
        4 |         22       43.55        1.64
        5 |         22       49.86        0.86
        6 |         20       46.40        1.15
        7 |         67       62.82        3.30
        8 |         21       49.67        2.10
        9 |         21       46.33        1.33
       10 |         20       47.85        1.60
----------------------------------------------

regress math

      Source |       SS       df       MS              Number of obs =     260
-------------+------------------------------           F(  0,   259) =    0.00
       Model |        0.00     0           .           Prob > F      =       .
    Residual |    32116.60   259  124.002317           R-squared     =  0.0000
-------------+------------------------------           Adj R-squared =  0.0000
       Total |    32116.60   259  124.002317           Root MSE      =  11.136

------------------------------------------------------------------------------
        math |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
       _cons |       51.3   .6906026    74.28   0.000     49.94009    52.65991
------------------------------------------------------------------------------

regress math hmwk

      Source |       SS       df       MS              Number of obs =     260
-------------+------------------------------           F(  1,   258) =   84.64
       Model |  7933.80702     1  7933.80702           Prob > F      =  0.0000
    Residual |   24182.793   258  93.7317557           R-squared     =  0.2470
-------------+------------------------------           Adj R-squared =  0.2441
       Total |    32116.60   259  124.002317           Root MSE      =  9.6815

------------------------------------------------------------------------------
        math |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
        hmwk |   3.571856   .3882366     9.20   0.000      2.80734    4.336372
       _cons |   44.07386    .988641    44.58   0.000     42.12703    46.02069
------------------------------------------------------------------------------

sort school
by school: generate i = _n
egen mmath = mean(math), by(school)
egen mhmwk = mean(hmwk), by(school)

regress mmath if i==1 [aw=n]
(sum of wgt is   2.6000e+02)

      Source |       SS       df       MS              Number of obs =      10
-------------+------------------------------           F(  0,     9) =    0.00
       Model |        0.00     0           .           Prob > F      =       .
    Residual |  539.635975     9  59.9595528           R-squared     =  0.0000
-------------+------------------------------           Adj R-squared =  0.0000
       Total |  539.635975     9  59.9595528           Root MSE      =  7.7434

------------------------------------------------------------------------------
       mmath |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
       _cons |       51.3   2.448664    20.95   0.000     45.76074    56.83926
------------------------------------------------------------------------------

regress mmath mhmwk if i==1 [aw=n]
(sum of wgt is   2.6000e+02)

      Source |       SS       df       MS              Number of obs =      10
-------------+------------------------------           F(  1,     8) =   14.33
       Model |  346.267285     1  346.267285           Prob > F      =  0.0054
    Residual |   193.36869     8  24.1710863           R-squared     =  0.6417
-------------+------------------------------           Adj R-squared =  0.5969
       Total |  539.635975     9  59.9595528           Root MSE      =  4.9164

------------------------------------------------------------------------------
       mmath |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
       mhmwk |   7.014745   1.853336     3.78   0.005     2.740944    11.28855
       _cons |   37.10863   4.058993     9.14   0.000     27.74858    46.46869
------------------------------------------------------------------------------

regress math hmwk mhmwk

      Source |       SS       df       MS              Number of obs =     260
-------------+------------------------------           F(  2,   257) =   67.00
       Model |  11006.6159     2  5503.30794           Prob > F      =  0.0000
    Residual |  21109.9841   257  82.1400161           R-squared     =  0.3427
-------------+------------------------------           Adj R-squared =  0.3376
       Total |    32116.60   259  124.002317           Root MSE      =  9.0631

------------------------------------------------------------------------------
        math |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
        hmwk |   2.136635   .4326083     4.94   0.000     1.284726    2.988543
       mhmwk |    4.87811    .797556     6.12   0.000     3.307533    6.448687
       _cons |   37.10863   1.467442    25.29   0.000     34.21889    39.99837
------------------------------------------------------------------------------

statsby "regress math hmwk" _b[_cons] _b[hmwk] , by(school) clear

command:     regress math hmwk
by:          school
statistics:  _stat1 = _b[_cons]
             _stat2 = _b[hmwk]

list

        school     _stat1     _stat2
  1.         1   50.68354  -3.553797
  2.         2   49.01229  -2.920123
  3.         3      38.75   7.909091
  4.         4   34.39382   5.592664
  5.         5   53.93863  -4.718411
  6.         6   49.25896  -2.486056
  7.         7   59.21022    1.09464
  8.         8   36.05535    6.49631
  9.         9      38.52       5.86
 10.        10   37.71392   6.335052

use sch10
eq l2_c: cons
eq l2_s: hmwk
set more off
gllamm math hmwk, i(school) nrf(2) eqs(l2_c l2_s) nip(8) adapt trace

General model information
-----------------------------------------------------------------------------

dependent variable:         math
family:                     gauss
link:                       ident
equation for fixed effects  hmwk _cons

Random effects information for 2 level model
-----------------------------------------------------------------------------

***level 1 equation:

   log standard deviation
   lns1: _cons

***level 2 (school) equation(s):
   (2 random effect(s))

number of level 1 units = 260
number of level 2 units = 10

Condition Number = 61.31589

gllamm model

log likelihood = -884.67624

------------------------------------------------------------------------------

        math |      Coef.   Std. Err.      z    P>|z|     [95% Conf.
Interval]
-------------+----------------------------------------------------------------

        hmwk |   2.052707   1.333179     1.54   0.124    -.5602752  4.665689
       _cons |   44.77742   2.541964    17.62   0.000     39.79526 49.75958
------------------------------------------------------------------------------


Variance at level 1
-----------------------------------------------------------------------------

  43.080053 (3.9372806)

Variances and covariances of random effects
-----------------------------------------------------------------------------


***level 2 (school)

    var(1): 63.854229 (29.718205)
    cov(1,2): -29.445939 (13.334485) cor(1,2): -.80583291

    var(2): 20.910824 (9.4002083)
-----------------------------------------------------------------------------

UCLA Department of Education

Phil Ender, 29Jan98