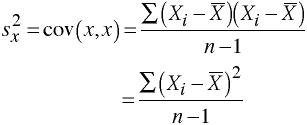
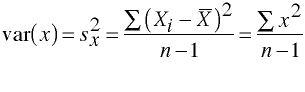
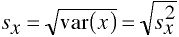
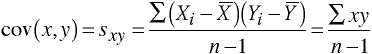
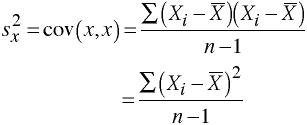
Plotting Two Variables Simultaneously
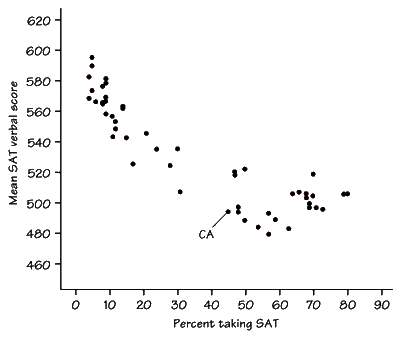
The more tightly the points are clustered together the higher the correlation between the two variables and the higher the ability to predict one variable from another.
Correlation coefficients can take on any value between -1 and +1, with + and - 1 representing perfect correlations between the variables. And a correlation of zero representing no relationship between the variables.
A rule of thumb for interpreting correlation coefficients:
Corr Interpretation 0 to .1 trivial .1 to .3 small .3 to .5 moderate .5 to .7 large .7 to .9 very large
Correlations are interpreted by squaring the value of the correlation coefficient. The squared value represents the proportion of variance of one variace that is shared with the other variable, in other words, the proportion of the variance of one variable that can be predicted from the other variable.
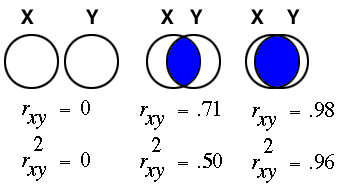
corr n .10 617 .20 153 .30 68 .40 37 .50 22 .60 15 .70 10 .80 7 .90 5
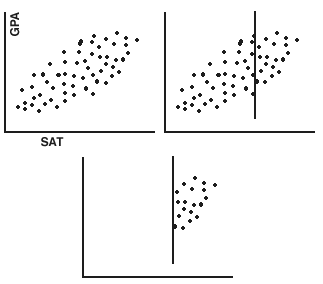
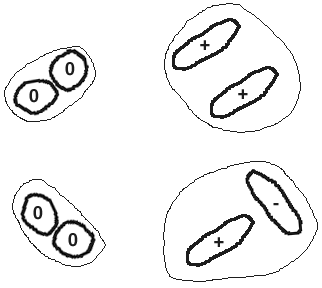
Sources of Misleading Correlation Coefficients
Restriction of Range
Extreme Groups
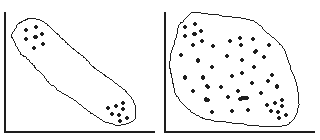
Combining Groups
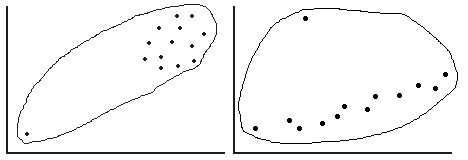
Outliers
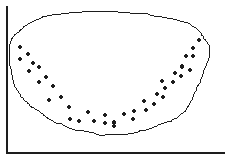
Curvilinearity
Discuss Correlation & Causation
Of course, just because two variables are correlated it does not mean that they are causally related. Often a third variable, a lurking variable, that is not included in the analysis is responsible (causes) for the first two variables. A lurking variable is a variable that loiters in the background and affects both of the original variables
Other Correlation Coefficients
Spearman Example
| Sub | xrank | yrank | d | d2 |
| a | 1 | 3 | -2 | 4 |
| b | 4 | 4 | 0 | 0 |
| c | 5 | 8 | -3 | 9 |
| d | 10 | 5 | 5 | 25 |
| e | 8 | 2 | 6 | 36 |
| f | 14 | 15 | -1 | 1 |
| g | 7 | 9 | -2 | 4 |
| h | 2 | 6 | -4 | 16 |
| i | 12 | 14 | -2 | 4 |
| j | 9 | 7 | 2 | 4 |
| k | 15 | 13 | 2 | 4 |
| l | 3 | 1 | 2 | 4 |
| m | 13 | 12 | 1 | 1 |
| n | 11 | 10 | 1 | 1 |
| o | 6 | 11 | -5 | 25 |
| Sum | 0 | 138 |
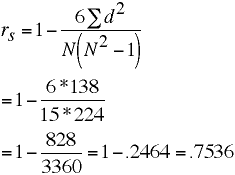
Stata Example
input xrank yrank
1 3
4 4
5 8
10 5
8 2
14 15
7 9
2 6
12 14
9 7
15 13
3 1
13 12
11 10
6 11
end
corr
(obs=15)
| xrank yrank
---------+------------------
xrank | 1.0000
yrank | 0.7536 1.0000
Another Stata Example
input y x
100 135
120 105
160 155
220 175
110 105
140 145
200 185
260 195
130 145
110 105
180 175
210 165
200 175
170 145
120 145
end
egen xrank = rank(x)
egen yrank = rank(y)
list
y x xrank yrank
1. 100 135 4 1
2. 110 105 2 2.5
3. 110 105 2 2.5
4. 120 145 6.5 4.5
5. 120 105 2 4.5
6. 130 145 6.5 6
7. 140 145 6.5 7
8. 160 155 9 8
9. 170 145 6.5 9
10. 180 175 12 10
11. 200 185 14 11.5
12. 200 175 12 11.5
13. 210 165 10 13
14. 220 175 12 14
15. 260 195 15 15
corr x y xrank yrank
(obs=15)
| y x xrank yrank
---------+------------------------------------
y | 1.0000
x | 0.8768 1.0000
xrank | 0.9118 0.9853 1.0000
yrank | 0.9821 0.8753 0.9073 1.0000
spearman x y
Number of obs = 15
Spearman's rho = 0.9073
Test of Ho: x and y independent
Pr > |t| = 0.0000
Point Biserial Correlation
Point Biserial Example
input y x
100 0
120 1
160 0
220 1
110 0
140 0
200 1
260 1
130 0
110 1
180 0
210 1
200 1
170 1
120 0
end
corr x y
(obs=15)
| x y
---------+------------------
x | 1.0000
y | 0.5541 1.0000
Fourfold Correlation - Phi Coefficient
| Y | ||||
| 1 | 0 | |||
| X | 1 | (a) 12 | (b) 16 | |
| 0 | (c) 14 | (d) 9 | ||
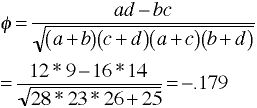
Stata Example
input x y w
0 0 9
0 1 14
1 0 16
1 1 12
end
corr x y [fw=w]
(obs=51)
| x y
---------+------------------
x | 1.0000
y | -0.1793 1.0000
tab x y [fw=w], all
| y
x | 0 1 | Total
-----------+----------------------+----------
0 | 9 14 | 23
1 | 16 12 | 28
-----------+----------------------+----------
Total | 25 26 | 51
Pearson chi2(1) = 1.6394 Pr = 0.200
likelihood-ratio chi2(1) = 1.6495 Pr = 0.199
Cramer's V = -0.1793
gamma = -0.3494 ASE = 0.252
Kendall's tau-b = -0.1793 ASE = 0.138
When analyzing two-by-two tables, the value of Cramer's V is actually phi. Cramer's V is a generalization of the phi coefficient that can be used in tables larger than two-by-two.