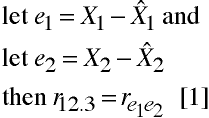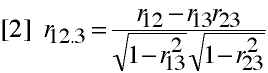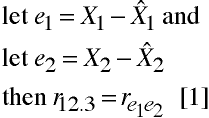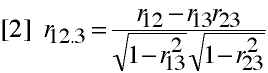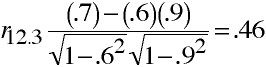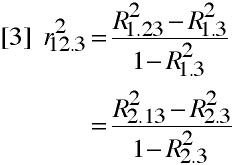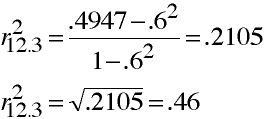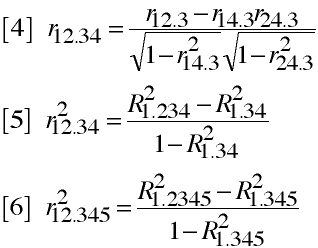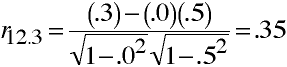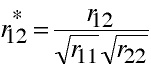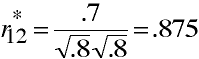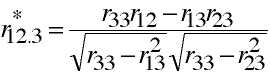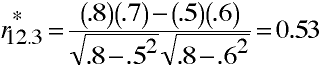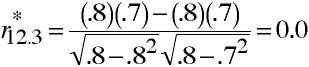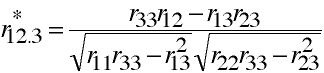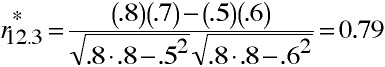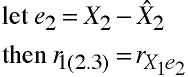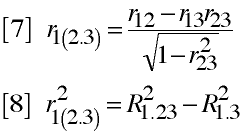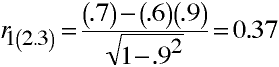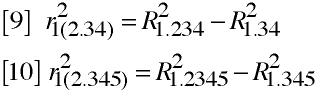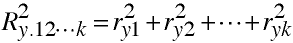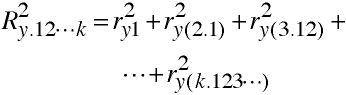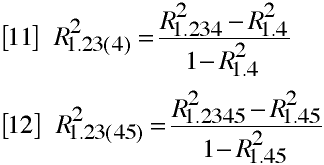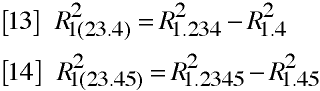Linear Statistical Models: Regression
Partial and Semipartial Correlation
Experimental Control
Controling variances by using equal groups.
Randomly assigning subjects to groups.
Conditions for all groups identical except for independent variable.
Statistical Control
Control variance by removing unwanted variance from other variables.
control by partialing.
Partial Correlation
r12.3 is the correlation between variables 1 and 2 with variable 3 removed from both
variables. To illustrate this, run separate regressions using X3 as the
independent variable and X1 and X2 as dependent variables. Next,
compute residuals for regression...
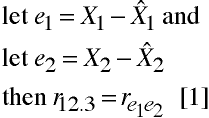
Venn Diagram of Partial Correlation
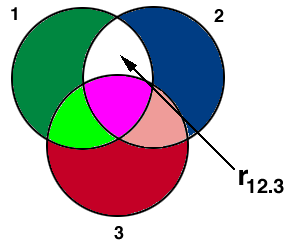
More Partial Correlation
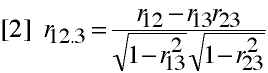
Example
Let r12 = 0.7; r13 = 0.6; r23 = 0.9.
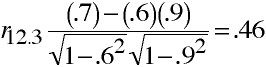
Using Multiple Correlations
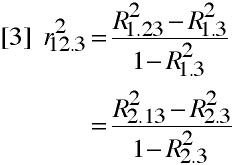
Thus, squared partial correlations represent the ratio of incremental variance to the
residual variance.
Example
Let R21.23 = .4947 and R21.3 = .62 = .36
(from the above example)
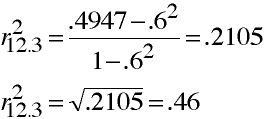
Higher Order Partial Correlation
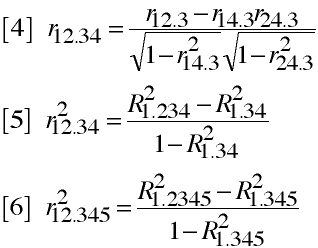
and so on...
Suppressor Variable
A special case when the partial correlation is larger than the zero-order correlation.
Zero or close to 0 correlation with the dependent variable.
Correlated with one or more independent variables.
Serves to suppress or control irrelevant variance.
Example
Let r12 = 0.3; r13 = 0.0; r23 = 0.5.
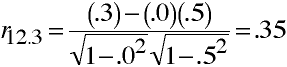
Let r212 = 0.09; r212.3 = 0.12;
Note: r212.3 is greater than r212 even
though r13 = 0.
Standardized regressions Coefficients: β2 = .4
and β3 = -.2
Note: suppressor variable receives a negative coefficient.
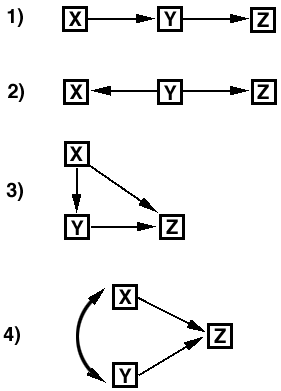
Causal Relationships
Partial correlation as a control method must be predicated on a sound theoretical framework.
Routine presentation of all higher-order partial correlations is a sign that theory
explaining the relationship among the variables is missing (Gordon, 1968).
With only three variables there are many possible causal models.
Measurement Error
Measurement error leads to biased estimates of zero-order and partial correlations.
Measurement error attenuates zero-order correlations.
Correction for Attenuation
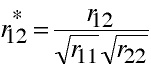
Example
When r12 = .7; r11 = r22 = .8
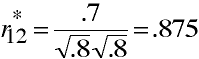
Correction for Attenuation in Partial Correlation
Partial correlation when correcting for unreliability in X3 only.
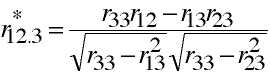
Example
When r12 = .7; r13 = .5; r23 = .6; r33 = .8;
and r12.3 = .58
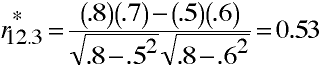
Another Example
When r12 = .7; r13 = .8; r23 = .7; r33 = .8;
and r12.3 = .33
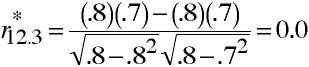
Correction for Attenuation in Partial Correlation
Partial correlation when correcting for unreliability in all measures.
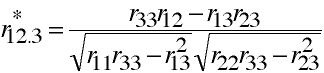
Example
When r12 = .7; r13 = .5; r23 = .6;
r11 = r22 = r33 = .8;
and r12.3 = .58
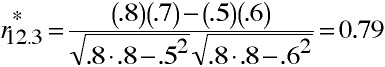
Semipartial Correlation
AKA -- part correlation.
r1(2.3) is the correlation between variables 1 and 2
with variation from variable 3 removed only from variable 2.
Compute residuals for X2
using X3 as the independent variable...
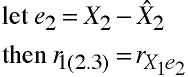
Venn Diagram of Semipartial Correlation
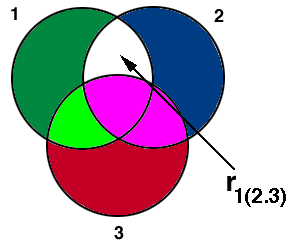
Semipartial Correlation Formulas
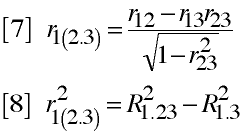
Thus, the squared semipartial correlation represents the proportion of variance of the dependent
variable accounted for by a given independent variable after another variable has already been
taken into account.
Example
r12 = .7; r13 = .6; r23 = .9
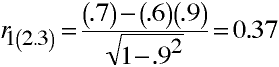
Remember
r21(2.3) does not necessarily equal r21(3.2)
since r21(2.3) = R21.23 - R21.3
and r21(3.2) = R21.23 - R21.2
Higher Order Semipartials
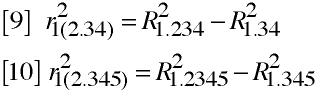
Regression & Semipartials
When independent variables are uncorrelated:
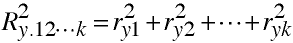
When independent variables are correlated:
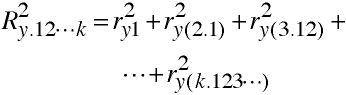
Multiple Partial Correlation
R21.23(4) is the squared multiple correlation of variable 1 with variables 2 and 3 after
the variation due to variable 4 has been partial out from all variables.
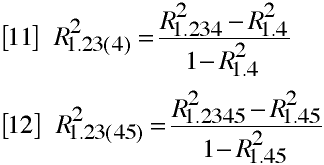
Multiple Semipartial Correlation
R21(23.4) is the squared multiple correlation of variable 1 with variables 2 and 3 after
the variation due to variable 4 has been partial out only from variables 2 and 3.
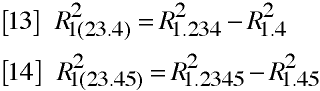
Partial & Semipartial Correlation in Stata
pcorr write read math science female
(obs=200)
Partial and semipartial correlations of write with
Partial Semipartial Partial Semipartial Significance
Variable | Corr. Corr. Corr.^2 Corr.^2 Value
------------+-----------------------------------------------------------------
read | 0.2567 0.1756 0.0659 0.0308 0.0003
math | 0.2925 0.2022 0.0855 0.0409 0.0000
science | 0.2792 0.1922 0.0779 0.0369 0.0001
female | 0.4239 0.3094 0.1797 0.0957 0.0000
partcorr write read, part(math science female) /* findit partcorr */
Response Variable: write
Predictor Variable(s): read
Partial Variable(s): math science female
Number of obs: 200
Coef Coef Squared
Mutiple Correlation = .59677648 .35614217
Partial Correlation = .25672403 .06590723
Semipartial Correlation = .17559606 .03083398
partcorr write read math, part(science female)
Response Variable: write
Predictor Variable(s): read math
Partial Variable(s): science female
Number of obs: 200
Coef Coef Squared
Mutiple Correlation = .66641064 .44410315
Partial Correlation = .47497762 .22560374
Semipartial Correlation = .35680815 .12731206
Linear Statistical Models Course
Phil Ender, 24sep10, 28Jan98