

Analyzing data that contain censored values or are truncated is common in many research disciplines. According to Hosmer and Lemeshow (1999), a censored value is one whose value is incomplete due to random factors for each subject. A truncated observation, on the other hand, is one which is incomplete due to a selection process in the design of the study. Thus, truncation changes the sample size while censoring does not.
We will begin by looking at analyzing data with censored values.
Regression with Censored Data
Regression models with censored data are sometimes called tobit models, named for the estimation that was originally developed by J. Tobin (1958).
The log likelihood for the general model with censored data looks like
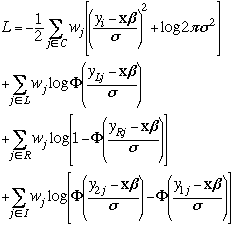
Let's start off with an example from Long (1997), the data are available from www.indiana.edu/~jsl650 (the data file is called job1tob.dta). This example looks at the prestige of a scientist's first job. Job prestige values were not available for departments without graduate programs or for graduate programs rated below 1.0. These cases were coded as ones. In this example, some of the ones represent 'true' ones, while the others are censored values that are less than one but whose 'true' values are unknown.
First we will looks at the OLS analysis with the censored data. With this approach all of the values scored as one are treated as if they were 'true' ones.
use http://www.gseis.ucla.edu/courses/data/job1tob
summarize jobcen0 jobcen1
Variable | Obs Mean Std. Dev. Min Max
-------------+-----------------------------------------------------
jobcen0 | 408 1.990784 1.31612 0 4.8
jobcen1 | 408 2.233431 .9736029 1 4.8
regress jobcen1 fem phd ment fel art cit
Source | SS df MS Number of obs = 408
-------------+------------------------------ F( 6, 401) = 17.78
Model | 81.0584763 6 13.5097461 Prob > F = 0.0000
Residual | 304.737915 401 .759944926 R-squared = 0.2101
-------------+------------------------------ Adj R-squared = 0.1983
Total | 385.796392 407 .947902683 Root MSE = .87175
------------------------------------------------------------------------------
jobcen1 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
fem | -.1391939 .0902344 -1.54 0.124 -.3165856 .0381977
phd | .2726826 .0493183 5.53 0.000 .1757278 .3696375
ment | .0011867 .0007012 1.69 0.091 -.0001917 .0025651
fel | .2341384 .0948206 2.47 0.014 .0477308 .4205461
art | .0228011 .0288843 0.79 0.430 -.0339824 .0795846
cit | .0044788 .0019687 2.28 0.023 .0006087 .008349
_cons | 1.067184 .1661357 6.42 0.000 .7405785 1.39379
------------------------------------------------------------------------------
listcoef
regress (N=408): Unstandardized and Standardized Estimates
Observed SD: .97360294
SD of Error: .8717482
---------------------------------------------------------------------------
jobcen1 | b t P>|t| bStdX bStdY bStdXY SDofX
---------+-----------------------------------------------------------------
fem | -0.13919 -1.543 0.124 -0.0680 -0.1430 -0.0698 0.4883
phd | 0.27268 5.529 0.000 0.2601 0.2801 0.2671 0.9538
ment | 0.00119 1.692 0.091 0.0778 0.0012 0.0799 65.5299
fel | 0.23414 2.469 0.014 0.1139 0.2405 0.1170 0.4866
art | 0.02280 0.789 0.430 0.0514 0.0234 0.0528 2.2561
cit | 0.00448 2.275 0.023 0.1481 0.0046 0.1521 33.0599
---------------------------------------------------------------------------
Next, we will perform an OLS regression after dropping out all of the cases that had been
censored to one. In this analysis, all of the ones are 'true' ones, the other values
are deleted. We have truncated the sample by dropping all prestige ratings less than
one.
regress jobcen0 fem phd ment fel art cit if jobcen0 ~= 0
Source | SS df MS Number of obs = 309
-------------+------------------------------ F( 6, 302) = 12.69
Model | 37.6365095 6 6.27275158 Prob > F = 0.0000
Residual | 149.290989 302 .494341024 R-squared = 0.2013
-------------+------------------------------ Adj R-squared = 0.1855
Total | 186.927499 308 .606907463 Root MSE = .70309
------------------------------------------------------------------------------
jobcen0 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
fem | .1014513 .0854827 1.19 0.236 -.0667658 .2696685
phd | .2973797 .0467477 6.36 0.000 .2053873 .3893722
ment | .0007784 .0006113 1.27 0.204 -.0004247 .0019814
fel | .1405303 .0897917 1.57 0.119 -.0361662 .3172269
art | .0058978 .0248279 0.24 0.812 -.0429598 .0547554
cit | .0021032 .0016553 1.27 0.205 -.0011542 .0053607
_cons | 1.412782 .1621386 8.71 0.000 1.093718 1.731846
------------------------------------------------------------------------------
listcoef
regress (N=309): Unstandardized and Standardized Estimates
Observed SD: .77904266
SD of Error: .70309389
---------------------------------------------------------------------------
jobcen0 | b t P>|t| bStdX bStdY bStdXY SDofX
---------+-----------------------------------------------------------------
fem | 0.10145 1.187 0.236 0.0481 0.1302 0.0618 0.4744
phd | 0.29738 6.361 0.000 0.2758 0.3817 0.3540 0.9274
ment | 0.00078 1.273 0.204 0.0541 0.0010 0.0695 69.5468
fel | 0.14053 1.565 0.119 0.0662 0.1804 0.0850 0.4710
art | 0.00590 0.238 0.812 0.0142 0.0076 0.0182 2.4000
cit | 0.00210 1.271 0.205 0.0760 0.0027 0.0976 36.1466
---------------------------------------------------------------------------
Finally, we will estimate a model using the tobit method. It includes those cases that were censored
to a value of one. We will declare the data to be left censored at 1.0. Using information in the
sample, the tobit procedure computes the probability that a value of one is censored and uses
the probability to aid in the estimation of the coefficients.
tobit jobcen1 fem phd ment fel art cit, ll(1)
Tobit estimates Number of obs = 408
LR chi2(6) = 89.20
Prob > chi2 = 0.0000
Log likelihood = -560.25209 Pseudo R2 = 0.0737
------------------------------------------------------------------------------
jobcen1 | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
fem | -.2368486 .1165795 -2.03 0.043 -.4660302 -.0076669
phd | .3225846 .0639198 5.05 0.000 .1969258 .4482435
ment | .0013436 .0008875 1.51 0.131 -.0004011 .0030884
fel | .3252657 .1224516 2.66 0.008 .0845403 .5659911
art | .0339053 .0365 0.93 0.353 -.0378493 .10566
cit | .00509 .0024751 2.06 0.040 .0002243 .0099557
_cons | .6854061 .218261 3.14 0.002 .2563307 1.114482
-------------+----------------------------------------------------------------
_se | 1.087237 .046533 (Ancillary parameter)
------------------------------------------------------------------------------
Obs. summary: 99 left-censored observations at jobcen1<=1
309 uncensored observations
listcoef
tobit (N=408): Unstandardized and Standardized Estimates
Observed SD: .97360294
Latent SD: 1.21966
SD of Error: 1.087237
---------------------------------------------------------------------------
jobcen1 | b t P>|t| bStdX bStdY bStdXY SDofX
---------+-----------------------------------------------------------------
fem | -0.23685 -2.032 0.043 -0.1156 -0.1942 -0.0948 0.4883
phd | 0.32258 5.047 0.000 0.3077 0.2645 0.2523 0.9538
ment | 0.00134 1.514 0.131 0.0880 0.0011 0.0722 65.5299
fel | 0.32527 2.656 0.008 0.1583 0.2667 0.1298 0.4866
art | 0.03391 0.929 0.353 0.0765 0.0278 0.0627 2.2561
cit | 0.00509 2.057 0.040 0.1683 0.0042 0.1380 33.0599
---------------------------------------------------------------------------
In the next example we have a variable called acadindx which is a weighted combination
of standardized test scores and academic grades. The maximum possible score on
acadindx is 200 but it is clear that the 26 students who scored 200 are not exactly
equal in their academic abilities. In other words, there is variability in
academic ability that is not being accounted for when students score 200 on
acadindx. Acadindx is right censored and in this sample, we do not know which students have
'true' scores of 200 and which ones have censored scores.We will begin by looking at a description of the data, some descriptive statistics, and correlations among the variables.
use http://www.gseis.ucla.edu/courses/data/acadindx2
(max possible on acadindx is 200)
describe
Contains data from acadindx.dta
obs: 200 max possible on acadindx is 200
vars: 5 19 Jan 2001 20:14
size: 4,800 (99.7% of memory free)
-------------------------------------------------------------------------------
1. id float %9.0g
2. female float %9.0g fl
3. reading float %9.0g
4. writing float %9.0g
5. acadindx float %9.0g academic index
-------------------------------------------------------------------------------
summarize
Variable | Obs Mean Std. Dev. Min Max
-------------+-----------------------------------------------------
id | 200 100.5 57.87918 1 200
female | 200 .545 .4992205 0 1
reading | 200 52.23 10.25294 28 76
writing | 200 52.775 9.478586 31 67
acadindx | 200 176.725 16.10485 143 200
count if acadindx==200
26
corr acadindx female reading writing
(obs=200)
| acadindx female reading writing
-------------+------------------------------------
acadindx | 1.0000
female | -0.0756 1.0000
reading | 0.7105 -0.0531 1.0000
writing | 0.6662 0.2565 0.5968 1.0000
Now, let's run a standard OLS regression on the data and generate predicted
scores in p1.
regress acadindx female reading writing
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 3, 196) = 106.87
Model | 32031.7937 3 10677.2646 Prob > F = 0.0000
Residual | 19582.0813 196 99.908578 R-squared = 0.6206
-------------+------------------------------ Adj R-squared = 0.6148
Total | 51613.875 199 259.366206 Root MSE = 9.9954
------------------------------------------------------------------------------
acadindx | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female | -5.436622 1.52325 -3.57 0.000 -8.440685 -2.432558
reading | .678742 .0893394 7.60 0.000 .5025521 .8549318
writing | .7672243 .0998418 7.68 0.000 .5703222 .9641263
_cons | 103.747 4.305933 24.09 0.000 95.2551 112.2389
------------------------------------------------------------------------------
predict p1
(option xb assumed; fitted values)
The tobit command is one of the commands that can be used for regression with
censored data. The syntax of the command is similar to regress with the addition
of the ul option to indication that the right censored value is 200. We will
follow the tobit command by generating p2 containing the tobit predicted values.
tobit acadindx female reading writing, ul(200)
Tobit estimates Number of obs = 200
LR chi2(3) = 191.51
Prob > chi2 = 0.0000
Log likelihood = -684.98404 Pseudo R2 = 0.1226
------------------------------------------------------------------------------
acadindx | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female | -6.279506 1.704417 -3.68 0.000 -9.64075 -2.918261
reading | .7863571 .1014259 7.75 0.000 .5863371 .986377
writing | .8102958 .110664 7.32 0.000 .5920577 1.028534
_cons | 97.30504 4.865994 20.00 0.000 87.70892 106.9012
-------------+----------------------------------------------------------------
_se | 10.91133 .5966562 (Ancillary parameter)
------------------------------------------------------------------------------
Obs. summary: 174 uncensored observations
26 right-censored observations at acadindx>=200
predict p2
(option xb assumed; fitted values)
Summarizing the p1 and p2 scores shows that the tobit predicted values have a larger
standard deviation and a greater range of values.
summarize acadindx p1 p2
Variable | Obs Mean Std. Dev. Min Max
-------------+-----------------------------------------------------
acadindx | 200 176.725 16.10485 143 200
p1 | 200 176.725 12.68715 148.2405 204.6992
p2 | 200 177.7175 14.07343 146.122 208.9989
When we look at a listing of p1 and p2 for all students who scored the maximum of 200
on acadindx, we see that in every case the tobit predicted value is greater than the
OLS predicted value. These predictions represents are an estimate of what the
variability would be if the values of acadindx could exceed 200.
list p1 p2 if acadindx==200
p1 p2
32. 183.6515 184.6332
39. 194.5114 197.2149
57. 196.3706 199.5261
61. 198.2299 201.8373
68. 204.6992 208.9989
80. 195.4331 198.6566
82. 192.0327 194.7362
88. 190.4983 193.1156
95. 199.3286 203.3269
100. 190.9407 193.2353
103. 195.2271 199.2036
132. 200.8631 204.9474
136. 193.1315 196.2257
143. 194.8429 197.8942
146. 188.6457 190.793
150. 163.7104 163.5542
154. 197.7348 201.0875
157. 195.1677 198.5848
161. 184.5666 186.0862
169. 186.344 188.3621
170. 183.2158 184.5022
174. 195.1677 198.5848
180. 196.3706 199.5261
192. 199.2693 202.7081
194. 189.4063 191.6147
200. 191.3316 194.5333
Here is the syntax diagram for tobit:
tobit depvar [indepvars] [weight] [if exp] [in range], ll[(#)] ul[(#)]
[ level(#) offset(varname) maximize_options ]
You can declare both lower and upper censored values. The censored values are fixed in that the same lower and upper values apply to all observations.
There are two other commands in Stata that allowed you more flexibility in doing regression with censored data.
cnreg estimates a model in which the censored values may vary from observation to observation.
intreg estimates a model where the response variable for each observation is either point data, interval data, left-censored data, or right-censored data.
It is also possible to estimate censored models using a semiparametric approach known as censored least absolute deviations (CLAD). We will demonstrate a CLAD solution with our last dataset using a Stata program clad (findit clad) that estimates the standard errors using the bootstrap method. CLAD procedures are espically useful in situations with heteroscedasticity, nonnormality or lack independence of the residuals.
clad acadindx female reading writing, ul(200) reps(200)
Initial sample size = 200
Final sample size = 189
Pseudo R2 = .41301816
Bootstrap statistics
Variable | Reps Observed Bias Std. Err. [95% Conf. Interval]
---------+-------------------------------------------------------------------
female | 200 -7.963542 1.273409 2.467652 -12.82964 -3.09744 (N)
| -11.29608 -1.762422 (P)
| -13.82872 -4.446603 (BC)
---------+-------------------------------------------------------------------
reading | 200 .7578125 -.0278584 .1388206 .4840643 1.031561 (N)
| .4333717 1.036449 (P)
| .5205993 1.069915 (BC)
---------+-------------------------------------------------------------------
writing | 200 .9505209 -.0278993 .1409488 .6725759 1.228466 (N)
| .6435294 1.223179 (P)
| .6999999 1.285714 (BC)
---------+-------------------------------------------------------------------
const | 200 92.375 1.748577 5.200157 82.12051 102.6295 (N)
| 84.47677 105.6032 (P)
| 82.63322 101.48 (BC)
-----------------------------------------------------------------------------
N = normal, P = percentile, BC = bias-corrected
I will reformat the output from tobit and clad to assist in comparing the results. I
have computed a t-test for clad although I am not sure the the coefficient divided by
the standard error is distributed as a t-statistic. I compute it just for comparison
purposes.
tobit model
------------------------------------------------------------------------------
acadindx | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female | -6.279506 1.704417 -3.68 0.000 -9.64075 -2.918261
reading | .7863571 .1014259 7.75 0.000 .5863371 .986377
writing | .8102958 .110664 7.32 0.000 .5920577 1.028534
_cons | 97.30504 4.865994 20.00 0.000 87.70892 106.9012
-------------+----------------------------------------------------------------
clad model
Variable | Observed Std. Err. t
---------+-------------------------------------------------------------------
female | -7.963542 2.467652 -3.23
reading | .7578125 .1388206 5.46
writing | .9505209 .1409488 6.74
const | 92.375 5.200157 17.76
-----------------------------------------------------------------------------
Regression with Truncated DataTruncated data occurs when some observations are not included in the analysis because of the value of the variable, that is, the sample is drawn from a restricted part of the populations. Truncation is a characteristic of the distribution from which the sample data are drawn. If x has a normal distribution with mean μ and standard deviation σ, then the density of the truncated normal distribution is
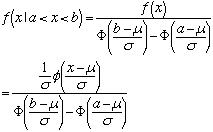
Compared with the mean of an untruncated variable, the mean of the truncated variable is greater if the truncation is from below, and is smaller if the truncation is from above. Furthermore, truncation reduces the variance compared with the variance of the untruncated distribution.
The log likelihood when a is the lower limit and b is the upper limit is
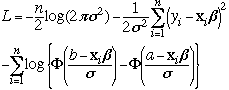
truncreg jobcen0 fem phd ment fel art cit, ll(1)
(note: 99 obs. truncated)
Truncated regression
Limit: lower = 1 Number of obs = 309
upper = +inf Wald chi2(6) = 71.13
Log likelihood = -318.66024 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
jobcen0 | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
eq1 |
fem | .114156 .095124 1.20 0.230 -.0722837 .3005956
phd | .3413744 .0539561 6.33 0.000 .2356224 .4471263
ment | .0008171 .0006589 1.24 0.215 -.0004743 .0021085
fel | .1709118 .1011169 1.69 0.091 -.0272737 .3690974
art | .0072712 .0271957 0.27 0.789 -.0460314 .0605738
cit | .0021862 .001788 1.22 0.221 -.0013182 .0056905
_cons | 1.187784 .1962769 6.05 0.000 .8030885 1.57248
-------------+----------------------------------------------------------------
sigma |
_cons | .7379857 .0353198 20.89 0.000 .6687602 .8072112
------------------------------------------------------------------------------
Next, we will analysis the dataset, acadindx, that was used in the previous section. If acadindx
is no longer loaded in memory you can obtain it with the following use command.
use http://www.gseis.ucla.edu/courses/data/acadindx2 (max possible on acadindx is 200)Let's imagine that in order to get into a special honors program, students need to score at least 165 on acadindx. So we will drop all observations in which the value of acadindx is less than 165.
drop if acadindx<165 (53 observations deleted)Now, let's estimate the same model that we used in the section on censored data, only this time we will pretend that a 200 for acadindx is not censored.
regress acadindx female reading writing
Source | SS df MS Number of obs = 147
-------------+------------------------------ F( 3, 143) = 35.17
Model | 7418.94448 3 2472.98149 Prob > F = 0.0000
Residual | 10053.7222 143 70.3057495 R-squared = 0.4246
-------------+------------------------------ Adj R-squared = 0.4125
Total | 17472.6667 146 119.675799 Root MSE = 8.3849
------------------------------------------------------------------------------
acadindx | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
female | -5.081622 1.491473 -3.41 0.001 -8.029805 -2.13344
reading | .4263403 .0874548 4.87 0.000 .253469 .5992115
writing | .5426893 .1062605 5.11 0.000 .3326451 .7527336
_cons | 132.9936 5.43257 24.48 0.000 122.2551 143.7322
------------------------------------------------------------------------------
It is clear that the estimates of the coefficients are distorted due to the fact that 53 observations
are no longer in the dataset. This amounts to restriction of range on both the response variable
and the predictor variables. What this means is that if our goal is to find the relation between
adadindx and the predictor variables in the popultions, then the truncation of acadindx in our
sample is going to lead to baised estimates. A better approach to analyzing these data is to use
truncated regression. In Stata this can be accomplished using the truncreg command where the ll
option is used to indicate the lower limit of acadindx scores used in the truncation.
truncreg acadindx female reading writing, ll(165)
(note: 3 obs. truncated)
Truncated regression
Limit: lower = 165 Number of obs = 144
upper = +inf Wald chi2(3) = 80.80
Log likelihood = -499.72027 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
acadindx | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
eq1 |
female | -5.264574 1.697022 -3.10 0.002 -8.590676 -1.938472
reading | .4429962 .1024458 4.32 0.000 .2422061 .6437862
writing | .6816854 .1324375 5.15 0.000 .4221128 .9412581
_cons | 123.6204 7.371454 16.77 0.000 109.1726 138.0681
-------------+----------------------------------------------------------------
sigma |
_cons | 8.817696 .625297 14.10 0.000 7.592136 10.04326
------------------------------------------------------------------------------
The coefficients from the truncreg command differ from the OLS and represent an attempt to adjust
the analysis for the arbitrary cutoff of acadindx scores at 165.
Categorical Data Analysis Course
Phil Ender